By Defne Guner
Is an Aristotelian denial of actual infinity justifiable considering our use of infinitary notions in mathematics?
Our modern understanding of limits in mathematics is closely linked to the Aristotelian concept of potential infinity. However, considering how limits are used within the definition of π, I will argue that denial of actual infinity cannot be justified in the light of how limits can be applied.
Aristotle differentiated between a potential and an actual infinity with the former referring to the always-existing possibility of a further step of division or addition. Aristotle writes in Physics that “something infinite will not be in actuality”, rejecting an actual infinity that exits “all at once” (Aristotle, 1969). For example, counting the natural numbers is a potential infinity since the next number can always be conceived by a person. The finite process of n + 1 is always possible, yet the potential infinity is never actualised since no human would be able to complete the potentially infinite process. Therefore, Aristotle would reject the conception of the natural numbers as an infinite set since it would represent an actual infinity that exists at a given time.
Following on from Aristotle’s argument, one can observe how the intuition behind potential infinity is necessary for our current understanding of the limits of sequences in mathematical analysis. It is generally accepted that a sequence an has a limit L, or converges to L, if and only if the terms of an get arbitrarily close to L (Easwaran, 2021). Limits of sequences are formally defined as:
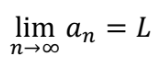
if and only if
for each real number ε > 0, there exists a natural number N, such that for every natural number
n > N, |an − L| < ε.
Similar to how Aristotle states a wooden plank is potentially infinite since it can be divided infinitely many times, but is not infinite in its existence, we can see how it is possible to approach a certain point through infinitely closer steps which is the intuition behind the
concept of limits. This Aristotelian example demonstrates that approaching a certain point sequentially (taking the limit of a sequence) is thought of as a potential infinity, as opposed to an actual infinity. The notation of n → ∞ only shows a direction and not an actual infinity.
Cantor opposed Aristotle, arguing that “…every potential infinite, if it is to be applicable in a rigorous mathematical way, presupposes an actual infinite (Cantor, 1887)”. To understand Cantor’s recognition of the actual infinite, we can consider infinite sequences such as the
decimal expansion of π. Considering the sequence xn where xi is equal to the decimal expansion of π up to (and including) the i’th digit, i.e., x3= 3.14. We can see through the process of enumerating the sequence that each term has the same number of digits as its index and that this process is a potential infinity since the next step is always possible. Each term in the sequence has a finite number of digits and each subsequent term has one more digit, thus, it is potentially infinite by addition according to Aristotle.
Since the sequence of finitely long terms gets arbitrarily close to π, we can conclude that it converges to π or that its limit is π. Hence, a sequence where the number of digits of subsequent terms is viewed as a potential infinity converges to a limit which is again a process
defined as potentially infinite. Each term of the sequence gets arbitrarily closer to a limit π, which would be recognised by Aristotle since the limit is never actually reached and the infinite steps are never completed. However, our modern mathematical understanding of the π recognises the number of digits of its decimal expansion as infinite. Furthermore, the number
of digits of π’s decimal expansion is not only a potential infinity through enumeration but also an actual infinity, π represents an actual infinity that exists at a given time.
Hence, we can see how the concept of limits is used to describe a potentially infinite sequence by a limit that is an actual infinity. Regarding Cantor’s argument, one can see how potential infinity presupposes an actual infinity in this example.
As argued by A. W. Moore in The Infinite, it is important to understand a contradiction within Aristotle’s denial of actual infinity: the infinitude of the past (Moore, 2018). Since Aristotle accepts the past to be potentially infinite, then he must also accept that it is actually infinite since at any given point the past can be thought of as a completed or traversed. The passing of time, a potential infinity, becomes an actual infinity when the past is considered. Similarly, the limit of the potentially infinite sequence xn, is π which is in actual infinity since the size of its decimal expansion is infinite.
Ludwig Wittgenstein urges his students to think about a person who had just finished reciting the entire decimal expansion of π backwards and he had started this task an “eternity” ago (Moore, 2018). Hence, the potentially infinite steps of reciting all the numbers have been already traversed. Although Wittgenstein’s hypothetical example might seem absurd, it demonstrates how infinity could be thought of as “completed” or “all together”. In our use of modern infinitary notions such as limits, we are able to utilise a similar way of thinking which makes the actual infinite necessary to accept.
To fully understand how limits are applied in our use of modern mathematics, we must also recognise an actual infinite. While Aristotle’s definition of potential infinity provides a very useful logical basis for understanding the concept of limits, his rejection of actual infinity restricts the application of this concept. Without recognising the actual infinite, how could we assign the limit of the sequence as π? Examining how π is the limit of a potentially infinite sequence xn, we can see that actual infinity is required within the use of limits for consistency Since we have shown how a potential infinity can converge into an actual infinity, the Aristotelian denial of actual infinity is no longer tenable.
References
Aristotle A. & Apostle H. G. (1969). Aristotle’s Physics. Indiana University Press.
Easwaran, K. A. (2021). The Infinity. (E. N. Zalta, Editor) Retrieved from The Stanford Encyclopedia of Philosophy: https://plato.stanford.edu/archives/win2021/entries/infinity/.
Hintikka, J. (1966). Aristotelian Infinity. The Philosophical Review: https://doi.org/10.2307/2183083.
Linnebo, Ø. & Shapiro, S. (2019). Actual and Potential Infinity. Noûs: https://0-doi-org.pugwash.lib.warwick.ac.uk/10.1111/nous.12208.
Moore, A. W. (2018). The Infinite. Routledge: https://0-doi-org.pugwash.lib.warwick.ac.uk/10.4324/9781315145921.
